- Coordinator: Tony Mancus
Numerical Weather Prediction
Learning objective: Use numerical models and their derivates in a good and responsible way
BIP-M regulations that will be covered:
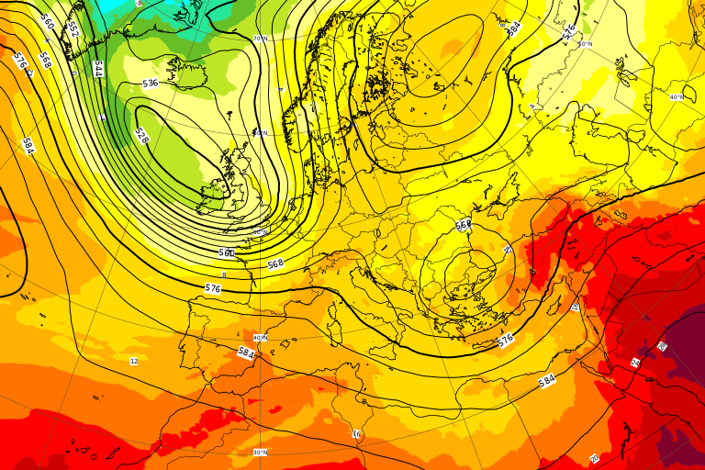
Principles of NWP data assimilation. Explain how information from observing networks and systems is obtained and prepared for use in an NWP model, and the principles behind objective analysis, data assimilation (including 3D-Var and 4D-Var) and initialization.
NWP forecast models. Describe the key components of an NWP model (including the prognostic variables, physical laws, and how physical processes are parameterized) and explain the difference between types of models (e.g., spectral versus grid point and hydrostatic versus non-hydrostatic models).
Strengths and weaknesses of NWP. Explain the strengths and weaknesses of NWP and the reasons why there are limits to atmospheric predictability.
Ensemble forecasting. Describe the principles behind ensemble forecasting and how such an approach can be used for short-, medium- and long-range forecasting.
Principles of downscaling. Describe the techniques used to provide detailed regional atmospheric information based on the output from global models.
Principles of post-processing and applications. Describe the techniques used for post-processing NWP output (e.g., use of model output statistics) and some of the applications driven by NWP output (e.g., wave and crop yield models).
Exams: Present weather briefing
Ensemble Prediction/Probabilistic Forecasting
Learning objectives: Understand how probabilistic forecasts are generated and verified,
and how they can be used and interpreted ; and Use probabilistic forecasts in a good
and responsible way while creating a weather forecast
BIP-M regulations that will be covered:
Ensemble forecasting. Describe the principles behind ensemble forecasting and how such an approach can be used for short-, medium- and long-range forecasting.
Post-processing and applications: Describe the techniques used for post-processing NWP output (for example, use of model output statistics).
Exams: A case study
- Coordinator: alan bol
- Coordinator: Tony Mancus
- Coordinator: Loren White