Beam Filling
The water drops which comprise the target are assumed to be evenly distributed throughout the entire sampling volume. That is not always true.
The radar beam diameter increases with range from the radar and depending on the target size and the radar beamwidth the target will not completely fill the radar beam at greater ranges.
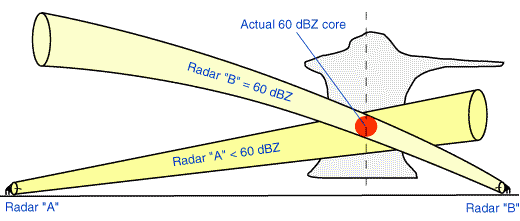
Different reflectivities can be calculated for the same target by two different radars in locations A and B.
In widespread stratiform precipitation, beam filling needs to be considered only in the vertical. For the direction of showers or thunderstorms, filling must be considered both horizontally and vertically. Some showers are less than one kilometre in width and even a one degree beam at 100 km may not be completely filled. High-based thunderstorms at close range may present beam-filling problems around their base if the beam elevation is not sufficiently high. In addition, the most intense precipitation portion of a storm may comprise only a small percentage of the storm volume.
A trap for the uninitiated are approaching frontal bands or even squall lines. At large distances the band can appear as a broad area of low reflectivity. But as it approaches the radar, convective elements “appear”. The truth of the matter is that the convective cells were probably always present, but not discernible on radar until they were able to fill the beam sufficiently.
One assumption made in the radar equation is that the precipitation target is composed of a very (small, large) number of (small, large) drops.
These drops are assumed to be (evenly, randomly) distributed throughout the sampling volume.
How much attenuation of energy is assumed to occur between the radar and the target (in dB)?
Two identical targets are scanned by a conventional weather radar. One target is centred at 20°/60 km and the other is centred at 70°/200 km. The target at 60 km just fills the beam. How will the reflectivities of the two targets compare? (closer target weaker than more distant target, targets have identical reflectivities, closer target stronger than more distant target).
Terms which describe the operating characteristics of particular radar are combined to generate the .
Since we do not know the actual characteristics of the precipitation target, the radar uses the measured average return power to estimate the of the target. If size, state, shape, and concentration of particles in the precipitation target were known, the could be derived, if all assumptions of the radar equation were met.
The radar (measures, estimates) reflectivity of a target and (measures, estimates) returned power from a target.
Reflectivity levels can be defined in terms of Ze and dBZe (true/false).