Radar Equation Continued

Factors of the Radar Equation elements illustrated in terms of the radar beam
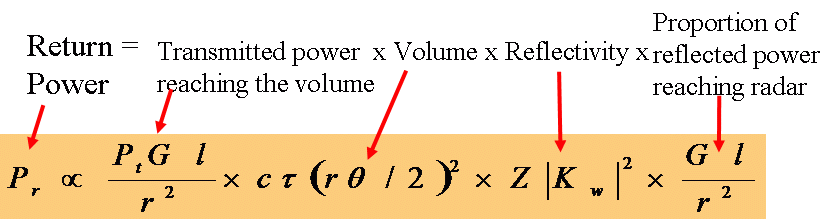
Assumptions made:
- Target drops satisfy Rayleigh scattering criterion: D < 0.07λ (= 3.5 or 7 mm)
- All precipitation droplets liquid water
- The beam is filled with evenly distributed droplets
- Negligible attenuation between radar and target – thus assuming l =1
The radar equation relates the returned power to the transmitted power, taking into account the focusing effect of the antenna, spherical geometry, the backscatter of the target and attenuation of the signal along the way. In most cases the attenuation is negligible and can be neglected, however it can have drastic consequences on the values measured, particularly in large hail situations at C band.
Full form of the Radar equation
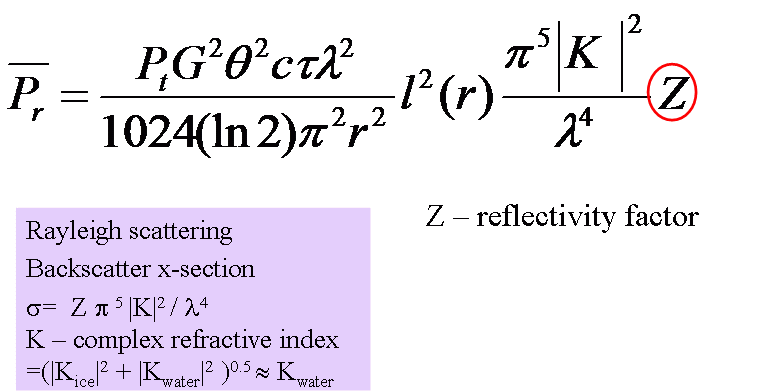
Constants:
- G – antenna gain
- Ae- antenna area = Gλ2/4π
- θ - beam width
- τ - pulse length
- 1/2ln(2) factor to allow for Gaussian beam shape
Neglect: l(r) – attenuation loss over path
If attenuation is neglected, then the remaining factors are constant for a given radar, and the equation can be simplified to an inverse square law (see below).
Simplified form of the Radar Equation
Most parameters are constants, and if assume no attenuation
returned power (Pr) ≈ reflectivity(Z) / distance2
or ↓

So reflectivity is obtained directly from returned power x square of the measured distance to the target.
Assume
- All reflecting particles are water spheres
- All scatterers obey Rayleigh scattering
- No multiple scattering, and
- Total average returned power = sum of powers scattered by individual particles – “effective reflectivity”
Rayleigh scattering valid for droplet diameters
- D< 0.05λ (water spheres)
- D< 0.1λ (ice spheres)
So,
At C band, Rayleigh scattering holds for D < 2.5mm (water) or <5mm (ice)
At S band, Rayleigh scattering holds for D < 5mm (water) or 10mm (ice)